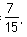从某学校高三年级男生随机抽取若干名测量身高,发现测量数据全部介于155cm和195cm之间且每个男生被抽取到
(I)在区间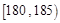
内的矩形的高为
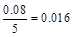
,在区间
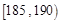
内的矩形的高为
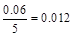
;(II)
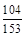
.
试题分析:(I)先利用已知及概率的性质求第六组、第七组的频率
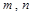
,再求在区间
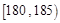
内的矩形的高和在区间
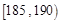
内的矩形的高,最后补充完整图形;(II)在(I)的基础上先求样本容量,再求最后三组人数,最后由古典概型求概率.
试题解析:(I)设第六组、第七组的频率分别为
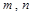
,得
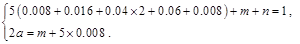
故
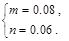
2分
在区间
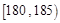
内的矩形的高为
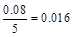
,在区间
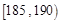
内的矩形的高为
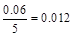
,补充完整图形. 4分
由题意可知,样本容量为
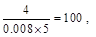
所以该校高三男生共有
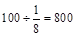
(人). 6分
估计该校高三年级全体男生身高不低于180cm的频率为
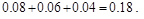
所以该校高三年级全体男生身高不低于180cm的人数为
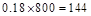
(人). 7分
(II)由(I)知,样本容量为100,最后三组人数分别为8,6,4(或用最后三组的比值求解),则所求的概率为

. 12分
(2010?济南二模)从某校高三年级800名男生中随机抽取50名学生测量其身高,据测量被测学生的身高全部在15
(1)由直方图可得前5组的概率是(0.008+0.016+0.04+0.04+0.06)×5=0.82,(1分)第8组的概率是0.04,所以第6,7组的概率是1-0.86=0.14,所以样本中6、7组的人数为7人.①(3分)
∵x,m,2成等差数列,
∴x=2m-2②?
由①②得:m=3,x=4,即y=0.08,n=0.06;z=0.016,p=0.012.频率分布直方图如图所示.(6分)
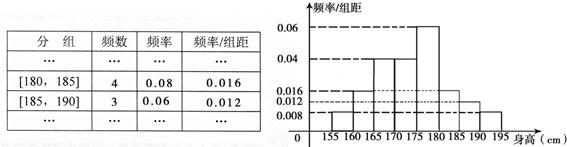
(2)由(1)知,?
身高在[180,185)内的人数为4人,设为a,b,c,d,身高在[190,195]内的人数为2人,设为A,B,(7分)?
若x,y∈[180,185)有ab,ac,ad,bc,bd,cd有6种情况;(8分)
x,y∈[190,195]有AB有1种情况,
若x,y∈[180,185)或x,y∈[190,195]时有aA,bA,cA,dA,aB,bB,cB,dB有8种情况.?高+考*资-源.网
所以基本事件总数为6+1+8=15种.(10分)?
所以,事件“|x-y|≤5”所包含的基本事件个数为6+1=7种,?
所以,P(|x-y|≤5)=715(12分)
某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材均介于155cm到195
(1)第六组的频率为450=0.08,第七组的频率为1-0.08-5×(0.008+0.016+0.04+0.04+0.06)=0.06;
(2)第六组的人数为4人,第一组的人数为50×5×0.008=2人,
从这6人中任意抽取2人,共有C26=15种抽法;
两人身高差距不超过5cm即随机抽取的2名男生在同一组,
∴两人身高差距不超过5cm的有C24+C22=7种抽法;
∴两人身高差距不超过5cm的概率为715.
唉,中国人都那么高吗?
不成熟的人,总说自己多么高大,真正长大了的人,反而却说自己如此矮小。这个,你能懂吗?
那些吧里的人十之八九都是炫耀自己长得很高,请问你见到过160的17岁男孩子在吧里畅谈吗?
我算是你哥哥了,我可以很负责任的告诉你,17岁的男孩子平均身高也就是171左右吧,你已经比较高了。
我22岁,我们这个年龄的平均身高也就是173,(或许还不到),而5年之后,当你22岁的时候,22岁的男孩子平均身高肯定会到175以上。
从某学校高三年级共800名男生中随机抽取50人测量身高。 据测量,被测学生身高全部介于155cm到195cm之间,
解:(I) 由频率分布直方图得组后三组频率为(0.016+0.012+0.008)×5=0.18这所学校高三年级全体男生身高在180 cm以上(含180 cm)的人数为800 ×0.18=144
(II)由已知得身高在[180,185)内的人数为4,
设为a、b、c、d,
身高在[190,195]内的人数为2,
设为A、B,若x,y∈[180,185)时,
有ab、ac、ad、bc、bd、cd共6种情况;
若x,y∈[190,195]时,有AB共1种情况;
若x,y分别在[180,185)和[190,195]内时,
有aA、bA、cA、dA、aB、bB、cB、dB,共8种情况.
所以,基本事件总数为6+1+8=15,
事件“|x-y|≤5”所包含的基本事件个数有6+1=7,所以P(|x-y|≤5)=